وب سایت رسم آنلاین نمودار
برای رسم توابع و دیدن شکل و نمودار توابع می توانید از سایت زیر استفاده کنید.
برای رسم توابع و دیدن شکل و نمودار توابع می توانید از سایت زیر استفاده کنید.
فیثاغورث در باره ی رابطه های عددی که درساختمانهای هندسی وجود دارد تحقیق می کرد . او مثلث معروف به مثلث مصری را ، که ضلعهای آن با عددهای 3و4و 5 بیان می شود ، را می شناخت .
مصریها می دانستند که چنین مثلثی قائم الزاویه است و ازآن برای تعیین زاویه های قائمه در تجدید تقسیم بندی زمینهای اطراف نیل ،که هر سال بر اثر طغیان آب شسته می شد، استفاده می کردند.
یکی از مشکلترین مسائل در ساختن اهرام و معبدها، طرح شالوده بنا به شکل مربع کامل بود که هم تراز باسطح افق باشد. جزئی اشتباه به قیمت از شکل افتادن همه ی بنا تمام می شد .
مصریان این مشکل رابا ساختن شاقول از میان برداشتند. نخستین شاقول احتمالاً تکه ریسمان یا نخی بود که وزنه ای به آن آویخته بودند و ان را در برابر بنا می گرفتند تا وزنه ی آن به زمین صاف برسد . در این حالت نخ می بایست کاملاً عمودیا شاقول باشد و زاویه ی بین آن و زمین صاف یک زاویه ی قائمه بسازد.
همچنین معماران کشف کردندکه چگونه می توان با ریسمان های اندازه گیری که درفاصله های مساوی گره خورده بودند، مثلثهای قائم الزاویه ای بسازند و این مثلثها را راهنمای خویش در ساختن گوشه ها ( نبش ها )ی بنا قرار دهند .
گام اول: براي خلاصه نويسي درس رياضي بايد فرمولها و قواعد همچنينرسم نمودارهاي لازم را يادداشت کنيم و هر مبحث را به طور جداگانه طبقه بندي نماييم.
گام دوم :براي هر مورد يک مثال يادداشت کنيم .
تذکر: چون اغلب قواعد، گاهي به وسيله موارد استثنايي و تبصرهها نقض ميشود، اين نکات خلاف قاعده نيز بايد يادداشت شود. در واقع، اهميت استثناها خيلي بيشتر است و عموما، سوالات مهم و اساسي در امتحانات دانشگاهها و کنکور از ميان اين مطالب استخراج ميگردد.
منبع: kanoon.ir
در ریاضیات تابع عملکردی است که برای هر ورودی داده شده یک خروجی منحصر بفرد تولید میکند معکوس این مطلب را در تعریف تابع بکار نمیبرند. یعنی در واقع یک تابع میتواند برای چند ورودی متمایز خروجیهای یکسان را نیز تولید کند. برای مثال با فرض y=x2 با ورودیهای 5- و 5 خروجی یکسان 25 را خواهیم داشت. در بیان ریاضی تابع رابطهای است که در آن عنصر اول به عنوان ورودی و عنصر دوم به عنوان خروجی تابع جفت شده است.
به عنوان مثال تابع f(x)=x2 بیان میکند که ارزش تابع برابر است با مربع هر عددی مانند x
 |
در واقع در ریاضیات رابطه را مجموعه جفتهای مرتب معرفی میکنند. با این شرط که هرگاه دو زوج با مولفههای اول یکسان در این رابطه موجود باشند آنگاه مولفههای دوم آنها نیز یکسان باشد. همچنین در این تعریف خروجی تابع را به عنوان مقدار تابع در آن نقطه مینامند. مفهوم تابع اساسی اکثر شاخههای ریاضی و علوم محاسباتی میباشد. همچنین در حالت کلی لزومی ندارد که ما بتوانیم فرم صریح یک تابع را به صورت جبری آلوگرافیکی و یا هر صورت دیگر نشان دهیم.
فقط کافیست این مطلب را بدانیم که برای هر ورودی تنها یک خروجی ایجاد میشود در چنین حالتی تابع را میتوان به عنوان یک جعبه سیاه در نظر گرفت که برای هر ورودی یک خروجی تولید میکند. همچنین لزومی ندارد که ورودی یک تابع ، عدد و یا مجموعه باشد. یعنی ورودی تابع را میتوان هر چیزی دلخواه در نظر گرفت البته با توجه به تعریف تابع و این مطلبی است که ریاضیدانان در همه جا از آن بهره میبرند.
نظریه مدرن توابع ریاضی بوسیله ریاضیدان بزرگ لایب نیتر مطرح شد همچنین نمایش تابع بوسیله نمادهای (y=f(x توسط لئونارد اویلر در قرن 18 اختراع گردید، ولی نظریه ابتدایی توابع به عنوان عملکرهایی که برای هر ورودی یک خروجی تولید کند توسط جوزف فوریه بیان شد. برای مثال در آن زمان فوریه ثابت کرد که هر تابع ریاضی سری فوریه دارد.
چیزی که ریاضیدانان ما قبل اوبه چنین موردی دست نیافته بودند، البته موضوع مهمی که قابل ذکر است آنست که نظریه توابع تا قبل از بوجود آمدن نظریه مجموعهها در قرن 19 پایه و اساس محکمی نداشت. بیان یک تابع اغلب برای مبتدیها با کمی ابهام همراه است، مثلا برای توابع کلمه x را به عنوان ورودی و y را به عنوان خروجی در نظر میگیرند ولی در بعضی جاها y,x را عوض میکنند.
ورودی یک تابع را اغلب بوسیله x نمایش میدهند. ولی زمانی که ورودی تابع اعداد صحیح باشد. آنرا با x اگر زمان باشد آنرا با t ، و اگر عدد مختلط باشد آنرا با z نمایش میدهند. البته اینها مباحثی هستند که ریاضیدانان برای فهم اینکه تابع بر چه نوع اشیایی اثر میکند بکار میرود. واژه قدیمی آرگومان قبلا به جای ورودی بکار میرفت. همچنین خروجی یک تابع را اغلب با y نمایش میدهند در بیشتر موارد به جای f(x) , y گفته میشود. به جای خروجی تابع نیز کلمه مقدار تابع بکار میرود. خروجی تابع اغلب با y نمایش داده میشود. ولی به عنوان مثال زمانی که ورودی تابع اعداد مختلط باشد، خروجی آنرا با "W" نمایش میدهیم. (W = f(z
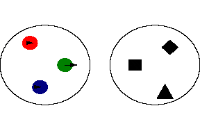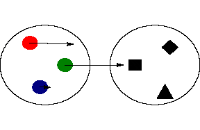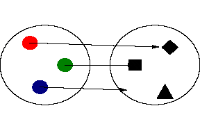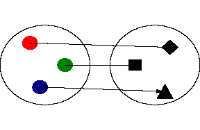
یک تابع رابطهای منحصر به فرد است که یک عضو از مجموعهای را با اعضای مجموعهای دیگر مرتبط میکند. تمام روابط موجود بین دو مجموعه نمیتواند یک تابع باشد برای روشن شدن موضوع ، مثالهایی در زیر ذکر میکنیم:
 |
این رابطه یک تابع نیست چون در آن عنصر 3، با دو عنصر ارتباط دارد. که این با تعریف تابع متناقص است چون برای یک عنصر از مجموعه، دو عنصر در مجموعه موجود است
 |
بطور ساخت یافته یک تابع از مجموعه x به مجموعه y بصورت f:x→y نوشته میشود و به صورت سه تایی مرتب ( (x,y,G(f) نمایش داده میشود. بطوری که (G(f زیر مجموعهای از حاصلضرب کارتزین xy میباشد. با این شرط که به ازای هر x در X یک Y متعلق به Y نسبت داد شود. با این شرط زوج مرتب (x,y) را در داخل (G(f میپذیریم. در این حالت نیز X را به عنوان دامنه f و y را به عنوان برد fو (G(f را به عنوان نمودار و یا گراف تابع F در نظر میگیرند.
توابع میتوانند:
منبع: دانشنامه رشد
بسیاری از ریاضیدانان قدیم عقیده داشتند که قوانین جادویی بر اعداد حکمفرماست.آنها سعی می کردند به این قوانین و روابط دست یابند و به این ترتیب بر دیگران برتری پیدا کنند.هنوز هم عده ای از مردم به این اعداد و نقش جادویی آنها اعتقاد دارند.
اگر می خواهید عدد جادویی نامتان را پیدا کنید با توجه به جدول به روش زیر عمل کنید:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | به جای حرف همزه بسته به مورد ی یا الف در نظر بگیرید. |
الف | ب | پ | ت | ث | ج | چ | ح | خ | |
د | ذ | ر | ز | ژ | س | ش | ص | ض | |
ط | ظ | ع | غ | ف | ق | ک | گ | ل | |
م | ن | و | ه | ی |
|
|
|
|
1-نام و نام خانوادگیتان را بنویسید.
۲-عدد هر حرف را زیر آن بنویسید.
3-عددها را با هم جمع کنید.
4-رقم های عدد به دست آمده را نیز با هم جمع کنید.
5-این کار را آن قدر ادامه دهید تایک عدد یک رقمی بین 1تا9به دست آید.
این عدد همان عدد جادویی نامتان است.
زاویه بین دو عقربه برابر است با:
( 30*ساعت -5/5 *دقیقه)
مثلا برای ساعت 12:20 عدد 5/5 را در 20 و30را 12 ضرب کنید. و حاصل ضرب ها را از هم کم کنید.پاسخ زاویه بین عقربه ها میشه
توجه:فرمول را از سمت چپ بخوانید

با سودکو 10 سال جوانتر شوید! سودوکو سرعت انتقال و تصمیم گیری در مغز را به نحو عجیبی افزایش می دهد، اول می توانید با پازل ها و جدولهای ساده که در تمام فروشگاه ها هست شروع کنید تا در سودوکو حرفه ای شوید!

|
بارم ریاضی 1 | ||||
|
عناوين |
پاياني نوبت اول |
پاياني نوبت دوم |
شهريور | |
|
از اعداد طبيعی تا پايان اعداد اعشاری |
5/1 |
1 |
2 | |
|
اعداد حقيقی- تقريب های اعشاری اعداد حقيقی |
1 | |||
|
نمادها و زبان رياضی |
5/1 | |||
|
از ابتدای فصل تا پايان تفاضل مجموعه ها |
5/1 |
- |
5/1 | |
|
مجموعه های متناهی و نامتناهی مشخص کردن مجموعه ها |
5/1 |
- | ||
|
توان رسانی وقواعدآن |
5/1 |
1 |
2 | |
|
نمادعلمی |
5/0 | |||
|
ريشه گيری |
5/1 | |||
|
تفريق و قرينة اعداد- تقسيم و معکوس اعداد |
5/0 |
2 |
3 | |
|
عبارت های جبری |
5/2 | |||
|
اتحادها و تجزيه |
3 | |||
|
معادله |
1 |
1 |
75/1 | |
|
رابطة خطی |
5/2 | |||
|
از شيب تا پايان خط های عمود برهم |
- |
5/2 |
25/2 | |
|
دستگاه معادلات خطی دو مجهولی- فاصلة دونقطه |
- |
5/1 | ||
|
نسبت های مثلثاتی |
- |
3 |
2 | |
|
ازابتدای فصل تا پايان ساده کردن عبارت های گويا |
- |
5/1 |
2 | |
|
از ابتدای تقسيم چندجمله ای ها تا پايان فصل |
- |
5/1 | ||
|
معادلات درجة دوم وحل آن ها |
- |
3 |
2 | |
|
نامعادلات درجة اول |
- |
2 |
5/1 | |
|
جمع |
20 |
20 |
20 | |
تذکر مهم:
توی کلاس فقط درمورد واحدهای درجه و رادیان صحبت شده و از واحد گراد سوال طرح نمی شود.
واحد های اندازه گیری زاویه:
واحد های اصلی برای اندازه گیری زاویه عبارتند از: درجه، گراد و رادیان که در اینجا به تعریف و توضیح آنها می پردازیم:
اگر محیط یک دایره دلخواه را به 360 قسمت مساوی تقسیم کنیم هر قسمت را یک درجه می نامند. به عبارت دیگر یک درجه یک سیصد و شستم محیط یک دایره است.
برای نمایش درجه از علامت  استفاده می شود. لذا می توان گفت:
استفاده می شود. لذا می توان گفت:

پس به این ترتیب در این مقیاس، زاویه تمام صفحه که یک دور کامل است برابر 360 درجه و زاویه نیم صفحه برابر 180 درجه است.
اجزای درجه:
همان گونه که می دانید معمولا هر واحد دارای اجزایی می باشد. درجه نیز به عنوان یک واحد اندازه گیری دارای اجزایی می باشد که عبارتند از دقیقه و ثانیه.(این اجزا گاهی آرک دقیقه:Arc minute و آرک ثانیه:Arc second نیز گفته میشوند)
هر دقیقه برابر است با یک شصتم درجه.
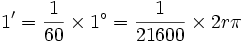
هر ثانیه برابر یک شصتم دقیقه یا یک سه هزار و شسصدم درجه.
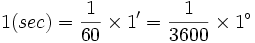
به عنوان مثال اگر اندازه زاویه ای 37 درجه و 30 دقیقه و 15 ثانیه باشد می نویسیم:
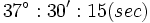
اگر محیط یک دایره را به 400 قسمت مساوی تقسیم کنیم هر قسمت را یک گراد می گویند. به عبارت دیگر یک چهارصدم دوران کامل، زاویهای به اندازه یک گراد پدید می آورد.گراد گاهی گون نیز گفته می شود. برای نمایش گراد از نماد «gr» استفاده می شود. لذا می توان گفت:

پس به این ترتیب در این مقیاس اندازه زاویه تمام صفحه یا یک دور کامل 400 گراد و اندازه زاویه نیم صفحه برابر 200 گراد خواهد بود.
اجزای گراد:
اجزای گراد عبارتند از دسی گراد(dgr) ، سانتی گراد(cgr)، میلی گراد(mgr) که هر کدام به ترتیب یک دهم گراد، یک صدم گراد و یک هزارم گراد می باشند.

به عنوان مثال اگر اندازه زاویه ای 37 گراد و 2 دسی گراد و 8 میلی گرا باشد می نویسیم:

استفاده از این واحد برای زاویه در ریاضیات بسیار کم است.
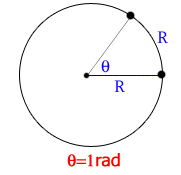
دایره ای به شعاع L را در نظر بگیرید. می دانیم محیط این دایره 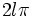 است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.
است. یک رادیان اندازه زاویه مرکزی مقابل به کمانی از دایره است که طول کمان روبرو به آن برابر شعاع دایره است.
برای نمایش رادیان از نماد«rad» استفاده می کنیم. بنابراین محیط هر دایره برحسب رادیان  رادیان است و زاویه نیم صفحه برابر
رادیان است و زاویه نیم صفحه برابر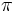 رادیان است. و لذا:
رادیان است. و لذا:  که در آن P محیط دایره است.
که در آن P محیط دایره است.
با استفاده از تعریف رادیان می توان نتیجه گرفت که اگر طول کمان روبرو به زاویه  برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد:
برابر s و شعاع دایره r باشد آنگاه اندازه زاویه تتا بر حسب رادیان را می توان با یک تناسب ساده چنین محاسبه کرد:
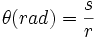
به عنوان مثال می خواهیم بدانیم اندازه زاویه مرکزی مقابل به کمانی از دایره که طول آن کمان 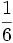 محیط دایره است چند رادیان است؟
محیط دایره است چند رادیان است؟
روش حل بدون استفاده از فرمول(اساس یافتن فرمول فوق) به این صورت است: r=طول شعاع
اگر طول کمان برابر 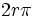 باشد آنگاه اندازه زاویه برابر است با
باشد آنگاه اندازه زاویه برابر است با  رادیان حال اگر
رادیان حال اگر
طول کمان برابر 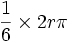 باشد اندازه زاویه چقدر می شود؟
باشد اندازه زاویه چقدر می شود؟

تبدیل واحد های اندازه گیری زاویه به یکدیگر:
دایره ای به شعاع r و زاویه 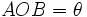 را در دایره در نظر بگیرید:
را در دایره در نظر بگیرید:
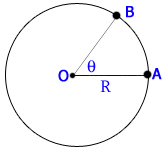
فرض کنید اندازه زاویه  برحسب درجه D، برحسب گراد G و برحسب رادیان R باشد. با استفاده از تناسب داریم:
برحسب درجه D، برحسب گراد G و برحسب رادیان R باشد. با استفاده از تناسب داریم:
1-
| طول کمان |
اندازه زاویه برحسب درجه |
|
|
360 |
|
|
D |
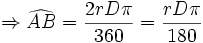
2-
|
طول کمان |
اندازه کمان برحسب گراد |
|
|
400 |
|
|
G |
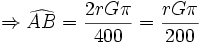
|
طول کمان |
اندازه زاویه برحسب رادیان |
|
|
 |
 |
R |
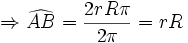
از تساوی های فوق رابطه زیر نتیجه می شود:
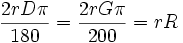

به عنوان مثال اگر اندازه زاویه ای برابر 20 گراد باشد اندازه این زاویه بر حسب درجه و رادیان به این صورت محاسبه میشود:
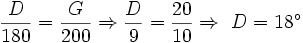
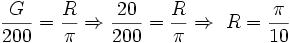

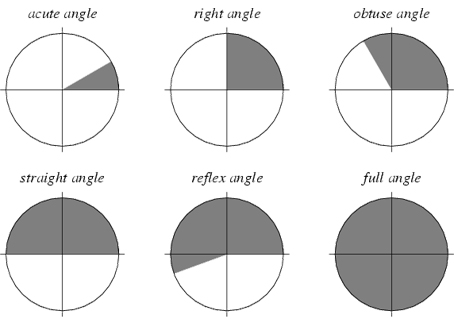
 را تند یا حاده میگوییم هرگاه اندازه اش کمتر از 90 در جه باشد. به عبارت دیگر:
را تند یا حاده میگوییم هرگاه اندازه اش کمتر از 90 در جه باشد. به عبارت دیگر: 
 را راست یا قائم میگوییم هرگاه اندازه آن برابر 90 در جه باشد. به عبارت دیگر:
را راست یا قائم میگوییم هرگاه اندازه آن برابر 90 در جه باشد. به عبارت دیگر: 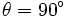
 را باز یا منفرجه می گوییم هرگاه بزرگتر از 90 درجه و کمتر از 180 درجه باشد. به عبارت دیگر:
را باز یا منفرجه می گوییم هرگاه بزرگتر از 90 درجه و کمتر از 180 درجه باشد. به عبارت دیگر: 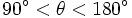
 را نیم صفحه میگوییم هرگاه برابر 180 درجه باشد. به عبارت دیگر:
را نیم صفحه میگوییم هرگاه برابر 180 درجه باشد. به عبارت دیگر: 
 را زاویه بازتاب میگوییم هرگاه بزرگتر از 180 درجه و کمتر از 360 درجه باشد. به عبارت دیگر:
را زاویه بازتاب میگوییم هرگاه بزرگتر از 180 درجه و کمتر از 360 درجه باشد. به عبارت دیگر: 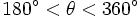
 را کامل یا تمام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر:
را کامل یا تمام صفحه می گوییم هرگاه برابر 360 درجه باشد. به عبارت دیگر: .
. 
شعاع درد مرا ضرب در عذاب كنيد
كه تا مساحت رنج مرا حساب كنيد
محيط تنگ دلم را شكسته رسم كنيد
خطوط منحني خنده را خراب كنيد
طنين نام مرا موريانه خواهد خورد
مرا به نام دگر غير من خطاب كنيد
دگر به منطق منسوخ مرگ مي خندم
مگر به شيوه ديگر مرا مجاب كنيد
در انجماد و سكون پيش از آنكه سنگ شوم
مرا به هرم نفسهاي عشق آب كنيد
مگر سماجت پولادي سكوت مرا
درون كوره فرياد خود مذاب كنيد
بلاغت غم من انتشار خواهد يافت
اگر كه متن سكوت مرا كتاب كنيد
برای توابع نیز مانند مجموعهها ، یا خود تناظرها میتوان عملیات جبری را تعریف نمود که باید تابع مورد نظر ، تابع حقیقی باشد. منظور از یک تابع با مقدار حقیقی روی مجموعه X، یا به طور خلاصه ، یک تابع حقیقی روی مجموعه X تابعی است مانند f: X→R از مجموعه X به مجموعه اعداد حقیقی، تابع مختلط نیز به طریق مشابهی تعریف میشود.
مجموعه دلخواه X را در نظر میگیریم؛ فرض میکنیم 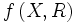 مجموعه کلیه توابع حقیقی روی مجموعه X باشد. برای این توابع حقیقی ، اعمال جمع و ضرب را نظیر اعمال جمع و ضرب در اعداد حقیقی میتوان تعریف نمود.
مجموعه کلیه توابع حقیقی روی مجموعه X باشد. برای این توابع حقیقی ، اعمال جمع و ضرب را نظیر اعمال جمع و ضرب در اعداد حقیقی میتوان تعریف نمود.
حاصل جمع دو تایی حقیقی f: X→R و g: X→R برابر است با تابع حقیقی f+g: X→R
به طوری که برای هر 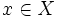 ، مقدار x تحت تابع f+g مساوی است با حاصل جمع دو عدد حقیقی
، مقدار x تحت تابع f+g مساوی است با حاصل جمع دو عدد حقیقی 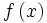 و
و 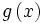 به عبارت دیگر ، برای هر
به عبارت دیگر ، برای هر 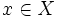 داریم:
داریم:
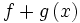 =
=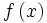 +
+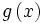
حاصلضرب دو تابع حقیقی f: X→R و g: X→R عبارت است از تابع حقیقی
fg: X→R به طوری که برای هر 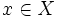 مقدار x تحت تابع fg برابر است با حاصلضرب دو عدد حقیقی
مقدار x تحت تابع fg برابر است با حاصلضرب دو عدد حقیقی 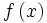 و
و 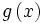 . به عبارت دیگر، برای هر
. به عبارت دیگر، برای هر 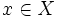 داریم:
داریم: 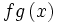 =
=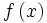 x
x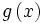
هرگاه تعداد عناصر مجموعه X باپایان باشد، با جمع و ضرب عناصر متناظر در جدول تناظر توابع g , f ، به آسانی میتوان جدول تناظر توابع f+g و fg را تشکیل داد.
حاصلجمع و حاصلضرب توابع حقیقی را به ترتیب حاصلجمع تابعی و حاصلضرب تابعی مینامیم. چون حاصلجمع و حاصلضرب توابع حقیقی براساس حاصلجمع و حاصلضرب اعداد حقیقی تعریف شدند، به سهولت خواص و ویژگیهای زیر را از اعداد حقیقی به ارث میبرند.
حاصلجمع تابعی و حاصلضرب تابعی توابع حقیقی دارای ویژگیهای زیر میباشند:
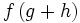 =
=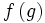 +
+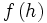
حاصلضرب عدد حقیقی C و تابع حقیقی f: X→R عبارت است از تابع حقیقی
Cf: X→R
به طوری که برای هر 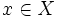 مقدار تابع برابر است با حاصلضرب دو عدد حقیقی C و
مقدار تابع برابر است با حاصلضرب دو عدد حقیقی C و 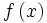
ویژگیهای مهم حاصلضرب عددی توابع حقیقی عبارتند از:
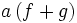 =af+ag
=af+ag 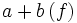 =af+bf
=af+bf 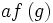 =
=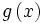
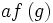 =
=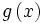
If=f
که در روابط بالا b , a اعداد حقیقی دلخواه و g , f توابع حقیقی دلخواهی روی مجموعه X میباشند.
تفاضل دو تابع حقیقی f: X→R و g: X→R را میتوان بر حسب حاصلضرب عددی و حاصلجمع تابعی به وسیله رابطه f-g=f+(-1)g
یا مستقیما، برای هر 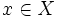 به وسیله:
به وسیله: 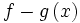 =
=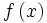 -
-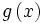 تعریف نمود.
تعریف نمود.
تفاضل f-g تابعی حقیقی روی مجموعه X میباشد.
خارج قسمت تابع حقیقی f: X→R بر تابع حقیقی g: X→R را میتوان برای هر 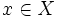 به صورت
به صورت
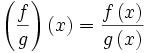
تعریف نمود. باید توجه داشت که تابع خارج قسمت (f/g) وقتی معین یا تعریف شده است که برای هر 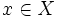 داشته باشیم g(x)≠0. بنابراین خارج قسمت f/g تابعی حقیقی روی مجموعه X میباشد.
داشته باشیم g(x)≠0. بنابراین خارج قسمت f/g تابعی حقیقی روی مجموعه X میباشد.
توانهای صحیح تابع حقیقی f: X→R یا به عبارت دیگر fn به این صورت تعریف میشود. هرگاه n>0 ، آنگاه fn ، تابع حقیقی بر روی مجموعه X است. که برای هر 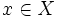 با ضابطه
با ضابطه
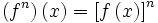
تعریف میشود. اگر n≤0، آنگاه برای هر 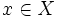 باید داشته باشیم
باید داشته باشیم 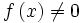 ، در این صورت ، fn برای هر
، در این صورت ، fn برای هر 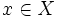 به صورت
به صورت 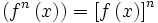 تعریف میشود.
تعریف میشود.
بنابراین، 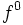 برابر تابع ثابت 1 روی مجموعه X خواهد بود.
برابر تابع ثابت 1 روی مجموعه X خواهد بود.
خواص توانهای صحیح حقیقی f: X→R، مستقیما از ویژگیهای متناظر اعداد حقیقی نتیجه میشود:
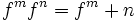
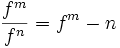
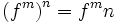
برای توابع جبری که ساختیم باید دامنه تعریف کنیم. دامنه توابع در زیر آمده است:
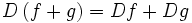

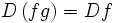
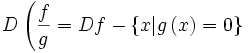
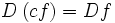

لطفا IQ خودتون رو در نظرات وبلاگ بذارید. البته با ذکر اسمتون.

مفهوم تایع یکی از مهم ترین مفاهیم علم ریاضی بوده و به همان اندازه در ریاضی اهمیت دارد که مفهوم مجموعه دارد.
اغلب، می گویند تابع، کمیت متغیری است که از کمیت متغیر دیگر تبعیت می کند. برای توزیع "معمولی"، مانند: y=sinx ,y=x2 , y=a+bx والی آخر، این تعریف کاملا مناسب می باشد.
ممکن است اگر توابع دیگری، مانند: y=sin2x+cos2x را در نظر بگیریم، می بینیم که مقادیر آن تابع دیگر تغییر نمی کند و بنابراین دیگر کمیت متغیری که از کمیت x تبعیت کند، وجود ندارد.
تعریف تایع:
تناظری که به هر عنصر x از یک مجموعه x فقط و فقط یک عنصر y از یک مجموعه y رانسبت را دهد، تایع گویند. توابع را با حروف f یا حروف کوچک خطی لاتین نشان می دهیم.
از طرفی، تحت عنوان کمیت "چیزهایی" را در نظر می گیرند که آنها همه با هم قابل مقایسه باشند. یعنی "چیزهایی که" بین آن ها روابط "بیشتر" و "کم تر" وجود دارد.
در صورتی که در ریاضیات، توابعی نیز مطالعه می شود که برای آنها این روابط تعیین نشده است، مثلا به عنوان مثال از اعداد کمپلکس (مختلط) یا به طور کلی از عناصر یک مجموعه دلخواه می توان اسم برد. توجه دقیق نشان می دهد که در مفهوم تابع وابستگی تغییرات به تغییرات متغیر مستقل آنم اندازه مهم نیست که تناظر بین مقادیر متغیر مستقل و مقادیر تابع مهم می باشد. به خصوص اگر به خاطر بیاوریم که تمامی اطلاعات راجع به تابع، می تواند از بیان گرافیکی آن استخراج گردد، و در نتیجه نباید فرض بین بیان گرافیکی تابع و خود تابع قائل شده و از طرفی
رافیک تابع مجموعه نقاطی است که هر یک از آن ها با دو مختصات y,x یعنی با (x,y) مشخص میگرند. بدین ترتیب به نظر می رسد که در تعریف تابع، مناسب است از آن خصوصیات مجموعه زوج های مرتب استفاده گردد که ویژه گرافیک تابع باشند.
مجموعه x را قلمرو تابع و مجموعه y را برد تابع f می نامند. تابعf را از مجموعه x به مجموعه y را معمولا به صورت f:x→y که (y=f(x نشان می دهند.
1) تبدیل درجه فارنهایت به سانتیگراد را در نظر می گیریم برای هر عدد حقیقی x، درجه فارنهایت معادل است با:
درجه سانتیگراد.
فرض می کنیم y,x هر دو عدد مجموعه اعداد حقیقی باشند، در نتیجه این عمل، به هر عنصر x از مجموعه Xعنصر یگانه (f(x از مجموعه y را نظیر می کند.
پس نتیجه می گیریم برای هر مقدار x یک مقدار x از منحصر بفردی y موجود است.
f(32)=0 f(68)= 0 f(212)=0
مفهوم تابع برای سه تایی مرتب:
در تابع f:X→Y مجموعه تمامی زوج هائی که اجزای اول آن ها را عناصر مجموعه X و اجزای دوم آن ها را تصویر عناصر مجموعه X تشکیل می دهند، گراف تابع خواهد بود.
برای توابع مفاهیمی مانند "گراف تابع"، "ناحیه مبدا تابع"، "ناحیه تعریف تابع"، "ناحیه مقادیر تابع" ظاهر می شود چون برای تابع، ناحیه تعریف با ناحیه مبدا منطبق می شود، بدین جهت برای تابع فقط ناحیه تعریف را به تنهایی به کار می برند. تابه f را با ناحیه تعریف x ناحیه مقصد y تابعی را "نوع x→y" می نامند.
تعبیر هندسی تابع:
f تابع است اگر خطی موازی محور y ها رسم کنیم منحنی تابع را فقط و فقط در یک نقطه قطع کند. یعنی به ازای یک y فقط و فقط یک x داشته باشیم.
زنگ آخر بود . از کلاس فرار کردم، از امتحان جبر!
در گوشه ای از حیاط ،خودم را گم و گور کردم. اما دلهره ی امتحان و جواب ندادن به سوالات جبر و نمره صفر ..
اکنون چند سال از آن روز می گذرد اما باز هم دلهره ی امتحان جبر آن روز را با خود دارم. به پسرم گفتم: «اگه بلد نیستی،اگه خواستی سر جلسه امتحان حاضر نشی، اشکالی نداره، یه راست بیا خونه، توی حیاط مدرسه نمون، یه وقت غصه نخوری بابا!»
پسرم با غرور در جوابم گفت: «نه بابا، مطمئن باش، با مجید، همکلاسیم، قرار گذاشتیم که جواب سوالات رو به همدیگه برسونیم.»
حالا چند ساعت از رفتن پسرم به مدرسه می گذرد اما دلهره ی جلسه ی امتحان رهایم نمی کند!
برای حل این مشکل از یک خط متقاطع استفاده کرده و این خط را به خط مماس نزدیک میکنیم.
برای درک بهتر موضوع به شکل زیر توجه کنید.
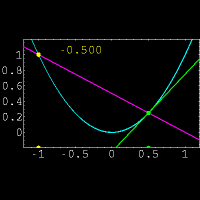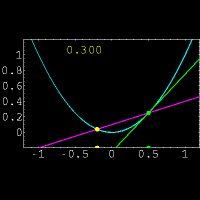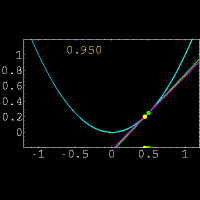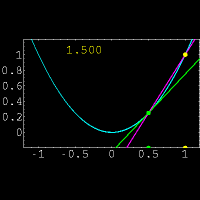
در این شکل خط متقاطع با رنگ بنفش و خط مماس با رنگ سبز مشخص شده است و عددی که در تصویر تغییر میکند نشان دهنده شیب خط متقاطع میباشد.
حال از دیدگاه ریاضی این روش را بیان میکنیم:
از دیدگاه ریاضی بدست آوردن مشتق با حد گیری از شیب خط قاطع که به خط مماس نزدیک شده است بدست می آید. پیدا کردن شیب نزدیکترین خط متقاطع به خط مماس با استفاده از کوچکترین h در فرمول زیر حاصل میشود:
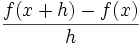
در این فرمول h به عنوان کوچکترین تغییر متغیر x تعریف میشودو میتواند مقدار مثبت یا منفی اختیار کند. در این فرمول شیب خط با استفاده از نقاط 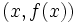 و
و 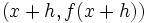 بدست می آید. واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ، حاصل حد زیر است:
بدست می آید. واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ، حاصل حد زیر است:
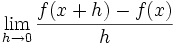
منبع:daneshnameh.roshd.ir
شخصی از امام علی (ع) پرسید: «عددی را به دست من بده که قابل قسمت بر ۲و ۳و ۴و ۵و ۶و ۷و ۸و ۹و ۱۰ باشد بی آنکه باقی بیاورد.»
امام علی علیه السلام بی درنگ به او فرمود: «اضرب ایام اسبوعک فی ایام سنتک»
یعنی: «روزهای هفته را بر روزهای یک سال خودت ضرب کن»
سوال کننده هفت را در ۳۶۰ ضرب کرد. حاصل آن یعنی ۲۵۲۰ بر تمام آن اعداد قابل قسمت بود بی آنکه باقی مانده بیاورد.
سه هزار سال پیش هر زمان که رودخانه بزرگ نیل طغیان می کرد، مزارع کشاورزی را زیر آب فرو می برد. پس از فرو کش کردن آب، دهقانان نمی توانستند زمینهای خود را شناسایی کنند و به همین دلیل بین آنها اختلافهای زیادی پیش می آمد. دانشمند آن زمان آهموس برای اولین بار به فکر افتاد تا با اندازه گیری مساحت زمینها و پیاده کردن شکل آنها روی کاغذ، چاره ای برای این مشکل پیدا کند. او مساحت زمینهای مختلف را که به شکلهای چهار گوش، سه گوش و شکلهای هندسی متنوعی بودند، با واحدهای اندازه گیری آن زمان اندازه گرفت.
آهموس پس از فرو نشستن آب، دوباره نقشه را پیاده می کرد و مزرعه هر کس را به هر شکل و مساحتی که پیش از آن داشت، به او تحویل می داد. به این ترتیب، اولین پایه های علم هندسه توسط آهموس بنا نهاده شد.
از طرف دیگر، مصریان آرامگاه بزرگان خود را به شکل هرم بنا می کردند. به همین علت نیز باید هندسه مقدماتی را برای طراحی و ساختن قبرها یاد می گرفتند. درباره قبر های پادشاهان و بزرگان مصر باستان، افسانه های زیادی گفته شده است. عده ای معتقدند که انسانها ی دیگر از کرات آسمانی به زمین آمده اند و نقشه معماری قبرها را به بیچارگان زمینی داده اند و آنان کار کشیده اند تا به خاطر حمله های آینده به زمین بتوانند از آنها کمک بگیرند .
هندسه در بیشتر زبانهاژؤ متری نام دارد.در زبان یونانی «ژؤ»به معنای زمین و«متری»به معنای اندازه گیری است.
سپس با آن نقاط یک بردار درست میشود که باید مختصات آن را نیز بنویسید.
اگر در هر مرحله با مشکل روبرو شدید می توانید پاسخ سوال را مشاهده کنید. البته هربار که دکمه دیدن پاسخ رو بزنید 20 امتیاز از دست میدهید.
برای دانلود بازی روی لینک زیر کلیک کنید.
فرض کنید که :
3+2=10
2+7=63
5+6=66
4+8=96
با این فرض ها ،فکر می کنید حاصل 9+7 چقدر است؟!