زندگی

شاید، آن روز که سهراب نوشت: 

"تا شقایق هست زندگی باید کرد..." 

خبر از دل پر درد گل یاس نداشت.

باید اینطور نوشت:

 "هر گلی هم باشی چه شقایق،چه گل پیچک و چه یاس زندگی اجباریست"

احساس

خندیدن خوب است

قهقهه عالیست!

گریســـتن آدم را آرام میکنـــد.

امــــــا...

لعنت بر بغــــــــض...!!!

دانش آموز باهوش

درکدام جنگ ناپلئون مرد؟ در آخرین جنگش

اعلامیه استقلال امریکا درکجا امضاشد؟ در پایین صفحه

چگونه می توانید یک تخم مرغ خام را به زمین بتنی بزنید بدون آن که ترک بردارد؟
زمین بتنی خیلی سخت است و ترک بر نمی دارد

علت اصلی طلاق چیست؟ ازدواج

علت اصلی عدم موفقیتها چیست؟ امتحانات

چه چیزهایی را هرگز نمی توان درصبحانه خورد؟ نهار و شام

چه چیزی شبیه به نیمی از یک سیب است؟ نیمه دیگر آن سیب

اگر یک سنگ قرمز را در دریا بیندازید چه خواهد شد؟ خیس خواهد شد

یک آدم چگونه ممکن است هشت روز نخوابد؟ 
مشکلی نیست شبها می خوابد

چگونه می توانید فیلی را با یک دست بلند کنید؟
شما امکان ندارد فیلی را پیدا کنیدکه یک دست داشته باشد

اگر در یک دست خود سه سیب و چهارپرتقال و در دست دیگر سه پرتقال و چهار سیب داشته باشید کلا چه خواهید داشت؟ 
دستهای خیلی بزرگ

اگر هشت نفر در ده ساعت یک دیوار را بسازند چهارنفر آن را در چند ساعت خواهند ساخت؟ 
هیچ چی چون دیوار قبلا ساخته شده !

درد دل

شوخی.........

بچه ها شوخی شوخی به پرنده ها سنگ میزنند ولی پرنده ها جدی جدی میمیرن 

ادما شوخی شوخی به هم زخم میزنند ولی قلب ها جدی جدی میشکنن 

تو شوخی شوخی به من لبخند زدی ولی من جدی جدی عاشقت شدم 

تو هم یه روزی شوخی شوخی تنهام میذاری منم جدی جدی ......

براي خلاصه برداري درس رياضي چکار کنيم؟

گام اول: براي خلاصه نويسي درس رياضي بايد فرمول‌ها و قواعد همچنينرسم نمودارهاي لازم را يادداشت کنيم و هر مبحث را به طور جداگانه طبقه بندي نماييم.

 

  گام دوم :براي هر مورد يک مثال يادداشت کنيم  .

 

تذکر: چون اغلب قواعد، گاهي به وسيله موارد استثنايي و تبصره‌ها نقض مي‌شود، اين نکات خلاف قاعده نيز بايد يادداشت شود. در واقع، اهميت استثناها خيلي بيشتر است و عموما، سوالات مهم و اساسي در امتحانات دانشگاه‌ها و کنکور از ميان اين مطالب استخراج مي‌گردد.

در ضمن پاسخگويي به سوالات رياضي مستلزم تکرار و تمرين زياد است .

منبع: kanoon.ir

نمودار توابع معروف ریاضی

ادامه مفهوم تابع

نکات اصلی:

1-مثالی برای ارائه ی مفهوم تابع: فرض کنید نام ۵ دانش آموز در دفتر نمره ی کلاس با اعداد ۱ تا ۵ مشخص شده باشد. وقتی می نویسیم (۱۷و۲) یعنی نفر شماره ی ۲ در امتحان ترم اول حسابان نمره ی ۱۷ گرفته است. کدام یک از مجموعه های زیر روش درستی برای نمایش نمرات حسابان است؟ 

2-در مثال بالا، در مجموعه ی A برای نفر دوم هم نمره 16 و هم نمره ی 17 منظور شده است، که چنین چیزی ممکن نیست. در واقع در مجموعه ی A نمره ی نفر دوم مبهم است؛ اما در مجموعه ی B چنین ابهامی وجود ندارد و نمره ی هر کس کاملاً مشخص است.

3-به مجموعه ای از زوجهای مرتب که هیچ ابهامی نداشته باشند (همانند B) یک تابع می گوییم. مجموعه ی A در مثال بالا تابع نیست(چرا؟). به طور دقیقتر:

4-تعریف اول تابع (تعریف کتاب ریاضی 2): تابع مجموعه ای از زوجهای مرتب است که مولفه های اول هیچ دو زوجی با یکدیگر برابر نباشند (و اگر دو زوج با مولفه های اول پیدا کردیم، باید مولفه های دوم نیز برابر باشند. به طور مثال  مجموعه ی یک تابع است.)

5-تعریف دوم تابع (تعریف کتاب حسابان): تابع f از مجموعه ی D به مجموعه ی R قاعده ای است که به هر عنصر x از D به نام دامنه، عنصر منحصر به فرد (f(x از مجموعه ی R به نام برد را نظیر می کند.

توضیح 1: در تعریف بالا به کلمات قرمز رنگ توجه کنید. در یک تابع باید از همه ی عناصر دامنه استفاده شود و به هر x از D دقیقاً یک عنصر از R منسوب شده باشد. 

توضیح 2: دقت کنید که در یک تابع لازم نیست از همه ی عناصر R استفاده شود.

6-تعاریف نکات ۴ و ۵ فرقی با یکدیگر ندارند.

7-اینجا یا اینجا و در شکلی که می بینید، مشخص کنید از بین 5 رابطه کدام تابع است و کدام تابع نیست و چرا. (توجه کنید که جهت خطوط ار چپ به راست است.)

8-تابع را می توان مانند یک ماشین تصور کرد که برای هر ورودی مجاز، یک خروجی منحصر به فرد دارد. (چرا؟)

9-قرار دادها و نمادها: اگر f تابعی با دامنه ی D و برد R باشد می نویسیم:

و می خوانیم f تابعی با دامنه ی D و برد R است که هر x از D را به (f(x از R تصویر می کند. (در واقع خروجی x از دستگاه f را (f(x می نامیم.) به ياضابطه یا قانون تابع f گوییم. دامنه ی f را معمولا با و برد f را معمولا با نمایش می دهیم.

مثال:

تابعی است که هر عنصر مجموعه ی  را ابتدا در ۲ ضرب و سپس با ۱ جمع می کند. به طور مثال و  ( یعنی تصویر ۰ تحت تابع f عدد ۱ و تصویر عدد 1- تحت تابع f عدد 1- است) و ضابطه ی این تابع .

مفهوم تابع

تعریف تابع

در ریاضیات تابع عملکردی است که برای هر ورودی داده شده یک خروجی منحصر بفرد تولید می‌کند معکوس این مطلب را در تعریف تابع بکار نمی‌برند. یعنی در واقع یک تابع می‌تواند برای چند ورودی متمایز خروجیهای یکسان را نیز تولید کند. برای مثال با فرض y=x² با ورودیهای 5- و 5 خروجی یکسان 25 را خواهیم داشت. در بیان ریاضی تابع رابطه‌ای است که در آن عنصر اول به عنوان ورودی و عنصر دوم به عنوان خروجی تابع جفت شده است.

به عنوان مثال تابع f(x)=x² بیان می‌کند که ارزش تابع برابر است با مربع هر عددی مانند x

در واقع در ریاضیات رابطه را مجموعه جفتهای مرتب معرفی می‌کنند. با این شرط که هرگاه دو زوج با مولفه‌های اول یکسان در این رابطه موجود باشند آنگاه مولفه‌های دوم آنها نیز یکسان باشد. همچنین در این تعریف خروجی تابع را به عنوان مقدار تابع در آن نقطه می‌نامند. مفهوم تابع اساسی اکثر شاخه‌های ریاضی و علوم محاسباتی می‌باشد. همچنین در حالت کلی لزومی ندارد که ما بتوانیم فرم صریح یک تابع را به صورت جبری آلوگرافیکی و یا هر صورت دیگر نشان دهیم.

فقط کافیست این مطلب را بدانیم که برای هر ورودی تنها یک خروجی ایجاد می‌شود در چنین حالتی تابع را می‌توان به عنوان یک جعبه سیاه در نظر گرفت که برای هر ورودی یک خروجی تولید می‌کند. همچنین لزومی ندارد که ورودی یک تابع ، عدد و یا مجموعه باشد. یعنی ورودی تابع را می‌توان هر چیزی دلخواه در نظر گرفت البته با توجه به تعریف تابع و این مطلبی است که ریاضیدانان در همه جا از آن بهره می‌برند.

تاریخچه تابع

نظریه مدرن توابع ریاضی بوسیله ریاضیدان بزرگ لایب نیتر مطرح شد همچنین نمایش تابع بوسیله نمادهای (y=f(x توسط لئونارد اویلر در قرن 18 اختراع گردید، ولی نظریه ابتدایی توابع به عنوان عملکرهایی که برای هر ورودی یک خروجی تولید کند توسط جوزف فوریه بیان شد. برای مثال در آن زمان فوریه ثابت کرد که هر تابع ریاضی سری فوریه دارد.

چیزی که ریاضیدانان ما قبل اوبه چنین موردی دست نیافته بودند، البته موضوع مهمی که قابل ذکر است آنست که نظریه توابع تا قبل از بوجود آمدن نظریه مجموعه‌ها در قرن 19 پایه و اساس محکمی نداشت. بیان یک تابع اغلب برای مبتدی‌ها با کمی ابهام همراه است، مثلا برای توابع کلمه x را به عنوان ورودی و y را به عنوان خروجی در نظر می‌گیرند ولی در بعضی جاها y,x را عوض می‌کنند.

ورودی تابع

ورودی یک تابع را اغلب بوسیله x نمایش می‌دهند. ولی زمانی که ورودی تابع اعداد صحیح باشد. آنرا با x اگر زمان باشد آنرا با t ، و اگر عدد مختلط باشد آنرا با z نمایش می‌دهند. البته اینها مباحثی هستند که ریاضیدانان برای فهم اینکه تابع بر چه نوع اشیایی اثر می‌کند بکار می‌رود. واژه قدیمی آرگومان قبلا به جای ورودی بکار می‌رفت. همچنین خروجی یک تابع را اغلب با y نمایش می‌دهند در بیشتر موارد به جای f(x) , y گفته می‌شود. به جای خروجی تابع نیز کلمه مقدار تابع بکار می‌رود. خروجی تابع اغلب با y نمایش داده می‌شود. ولی به عنوان مثال زمانی که ورودی تابع اعداد مختلط باشد، خروجی آنرا با "W" نمایش می‌دهیم. (W = f(z

تعریف روی مجموعه‌ها

یک تابع رابطه‌ای منحصر به فرد است که یک عضو از مجموعه‌ای را با اعضای مجموعه‌ای دیگر مرتبط می‌کند. تمام روابط موجود بین دو مجموعه نمی‌تواند یک تابع باشد برای روشن شدن موضوع ، مثالهایی در زیر ذکر می‌کنیم:

این رابطه یک تابع نیست چون در آن عنصر 3، با دو عنصر ارتباط دارد. که این با تعریف تابع متناقص است چون برای یک عنصر از مجموعه، دو عنصر در مجموعه موجود است

• این رابطه یک تابع یک به یک است. چون به ازای هر x یک y وجود دارد.

تعریف ساخت یافته تابع

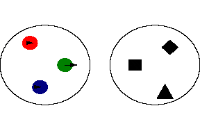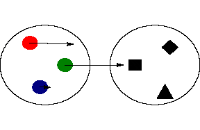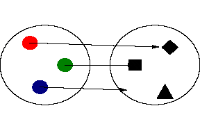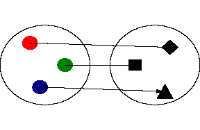بطور ساخت یافته یک تابع از مجموعه x به مجموعه y بصورت f:x→y نوشته می‌شود و به صورت سه تایی مرتب ( (x,y,G(f) نمایش داده می‌شود. بطوری که (G(f زیر مجموعه‌ای از حاصلضرب کارتزین xy می‌باشد. با این شرط که به ازای هر x در X یک Y متعلق به Y نسبت داد شود. با این شرط زوج مرتب (x,y) را در داخل (G(f می‌پذیریم. در این حالت نیز X را به عنوان دامنه f و y را به عنوان برد fو (G(f را به عنوان نمودار و یا گراف تابع F در نظر می‌گیرند.

خواص توابع

توابع می‌توانند:

• زوج یا فرد باشند.
• پیوسته یا ناپیوسته باشند.
• حقیقی یا مختلط باشند.
• اسکالر یا برداری باشند.

منبع: دانشنامه رشد